稀疏数组场景举例
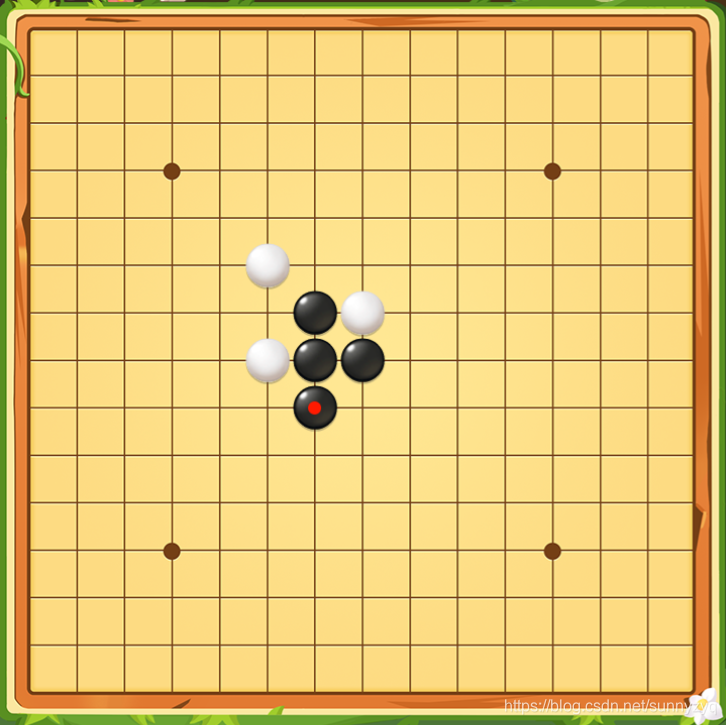
保存上图 15 x 15 的棋盘数据,通常情况下要创建一个二维数组,0代表空白,1代表白子,2代表黑子,得到的结果为

但是不足的是,有价值的数据就8个**(数据不关心是否重复),所以实际上保存的时候,使用稀疏数组将有价值的数据保存,这样会节省存储空间大小,如果要将数据写入磁盘,还会减少IO的读写量,提高性能
使用稀疏数组后的数组结果为
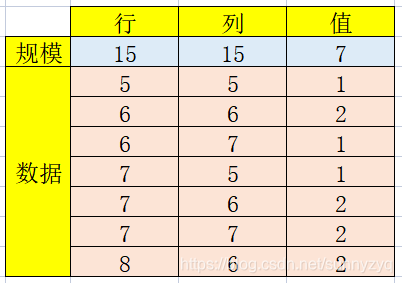
- 上图稀疏数组中,规模的行表示原二维数组有多少行,规模的列表示原二维数组有多少列,规模的值表示原二维数组有多少个有效值,数据模块则用来表示原二维数组有效数据的具体坐标以及值
二维数组和稀疏数组的转换
二维数组 =》 稀疏数组
- 遍历原始二维数组,得到有效值的个数sum
- 根据sum创建稀疏数组 int[sum + 1] [3]
- 原始二维数组行数、列数、有效值个数存到系数数组规模中
- 遍历原始二维数组,将有效数据存放到稀疏数组中
稀疏数组 =》 二维数组
- 读取稀疏数组规模,创建原二维数组的规模 int [15] [15]
- 读取稀疏数组数据,赋值给原二维数组
完整代码
javapackage sparse_array; public class SparseArray { public static void print(int[][] arr) { for (int i = 0; i < arr.length; i++) { for (int j = 0; j < arr[i].length; j++) { System.out.print(arr[i][j] + "\t"); } System.out.println(); } System.out.println("---------------------"); } public static void main(String[] args) { int[][] twoDimensionsArray = new int[15][15]; // 保存白子(用1表示) twoDimensionsArray[5][5] = 1; twoDimensionsArray[7][5] = 1; twoDimensionsArray[6][7] = 1; // 保存黑子(用2表示) twoDimensionsArray[6][6] = 2; twoDimensionsArray[7][6] = 2; twoDimensionsArray[8][6] = 2; twoDimensionsArray[7][7] = 2; // 将二维数组转成稀疏数组 int[][] sparseArray = twoDimensionToSparseArray(twoDimensionsArray); print(sparseArray); // 将稀疏数组转成二维数组 sparseArrayToTwoDimension(sparseArray); print(twoDimensionsArray); } /*** * @description: 二维数组 转 稀疏数组 * @author: ZhangHL * @date: 2025/2/5 17:42 * @param: [array] * @return: int[][] * * 1. 遍历原始二维数组,得到有效值的个数sum * 2. 根据sum创建稀疏数组 int[sum + 1] [3] * 3. 原始二维数组行数、列数、有效值个数存到系数数组规模中 * 4. 遍历原始二维数组,将有效数据存放到稀疏数组数据中 **/ public static int[][] twoDimensionToSparseArray(int[][] twoDimensionsArray) { // 1. 获取有效值的个数 int sum = 0; for (int i = 0; i < twoDimensionsArray.length; i++) { for (int j = 0; j < twoDimensionsArray[i].length; j++) { if (twoDimensionsArray[i][j] != 0) { sum++; } } } // 2. 根据sum创建数组 int[][] sparseArray = new int[sum + 1][3]; // 3. 将二维数组的行数、列数、有效值个数存到稀疏数组中 sparseArray[0][0] = twoDimensionsArray.length; // 二维数组行数 sparseArray[0][1] = twoDimensionsArray[0].length; // 二维数组列数 sparseArray[0][2] = sum; // 有效值个数 // 4. 将二维数组的有效值存到稀疏数组中 int sparseRow = 1; for (int i = 0; i < twoDimensionsArray.length; i++) { for (int j = 0; j < twoDimensionsArray[i].length; j++) { if (twoDimensionsArray[i][j] != 0) { sparseArray[sparseRow][0] = i; sparseArray[sparseRow][1] = j; sparseArray[sparseRow][2] = twoDimensionsArray[i][j]; sparseRow++; } } } return sparseArray; } /*** * @description: 稀疏数组 转 二维数组 * @author: ZhangHL * @date: 2025/2/5 17:42 * @param: [array] * @return: int[][] * * 1. 读取稀疏数组规模,创建原二维数组的规模 int [15] [15] * 2. 读取稀疏数组数据,赋值给原二维数组 **/ public static int[][] sparseArrayToTwoDimension(int[][] sparseArray) { // 原二维数组的总行数 int totalRow = sparseArray[0][0]; // 原二维数组的总列数 int totalCol = sparseArray[0][1]; int[][] twoDimensionsArray = new int[totalRow][totalCol]; for (int i = 1; i < sparseArray.length; i++) { int row = sparseArray[i][0]; int col = sparseArray[i][1]; int val = sparseArray[i][2]; twoDimensionsArray[row][col] = val; } return twoDimensionsArray; } }
队列的定义
- 队列是一个有序列表,可以使用数组或者链表实现,队列遵循**FIFO(先进先出)**的原则
数组实现简单队列
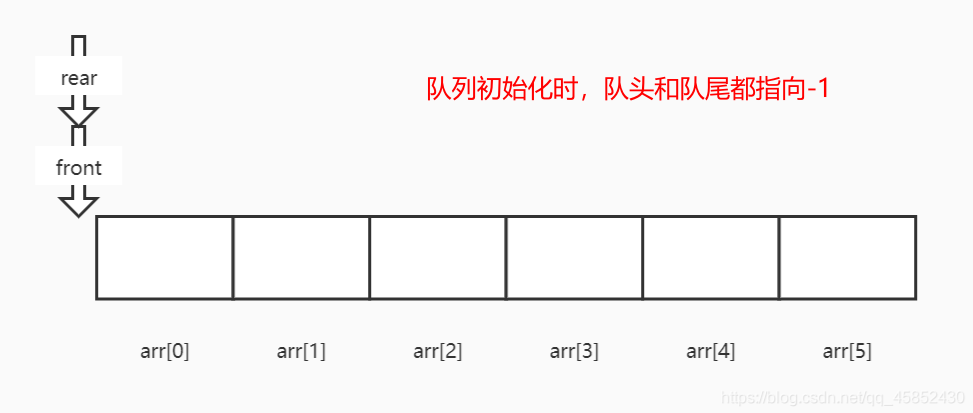
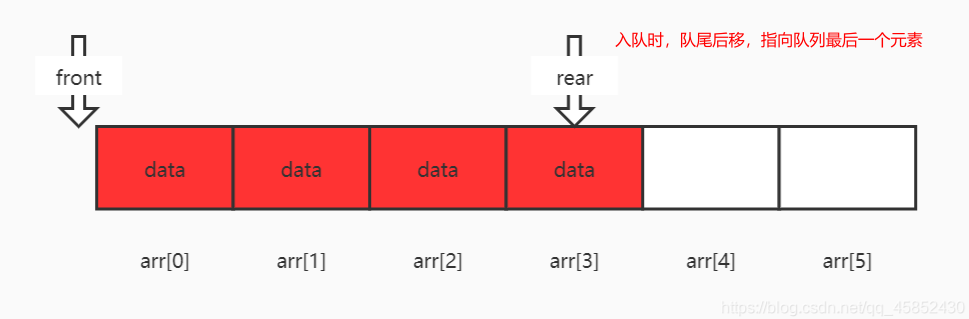
队列初始化、入队、出队情况如下
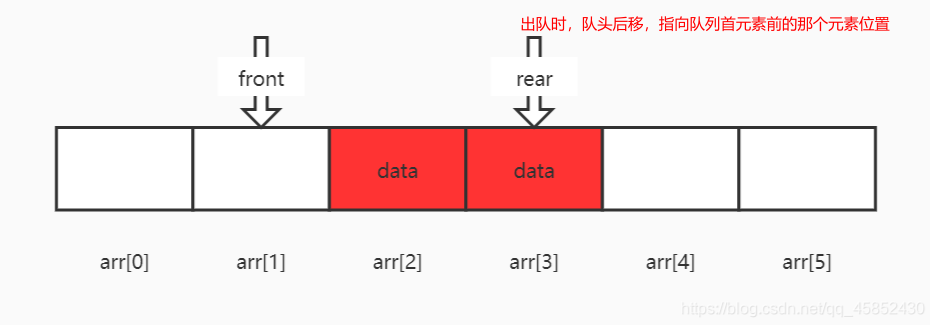
实现思路
- 既然要用一个数组实现队列,那么数据的存储方式就是一个数组
- 创建队列时要指定队列的最大长度
- 在考虑到队列入队和出队的需要,所以需要一个头指针和尾指针,入队时尾指针后移,出队时头指针后移
- 约定:队头指向队列中第一个元素之前的元素(初始值为-1),队尾指向队列中最后一个元素(初始值为-1)
完整代码
javaclass ArrayQueue { // 队列数据 private int[] data; // 队列最大长度 private int maxSize; // 头指针 private int front; // 尾指针 private int rear; // 判断队列是否已满 public boolean isFull() { return rear == maxSize - 1; } // 判断队列是否为空 public boolean isEmpty() { return rear == front; } // 入队 public void addQueue(int item) { if (isFull()) { throw new RuntimeException("队列已满,无法添加元素"); } rear++; data[rear] = item; } // 出队 public int getQueue() { if (isEmpty()) { throw new RuntimeException("队列为空,无法出队"); } front++; return data[front]; } // 获取队头元素(只获取,不出队) public int getQueueHeadItem() { if (isEmpty()) { throw new RuntimeException("队列为空,无法获取队头元素"); } return data[front + 1]; } // 获取元素个数 public int size() { return rear - front; } public ArrayQueue(int maxSize) { this.maxSize = maxSize; data = new int[maxSize]; front = -1; rear = -1; } }缺点
- 当队列已满,rear指向了data[maxSize - 1],然后数据全部出队,front也会指向data[maxSize - 1],如果再进行插入时,通过判断rear == maxSize - 1报队列已满,实际上指针前面的位置都是空的,因此该数组实现的队列的缺点是只能使用一次
数组实现环形队列(传统方式:牺牲一个空间)
目标:解决简单队列只能使用一次的缺点
队列初始化、队满情况如下
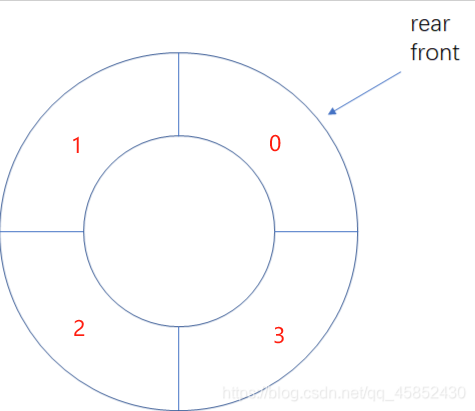
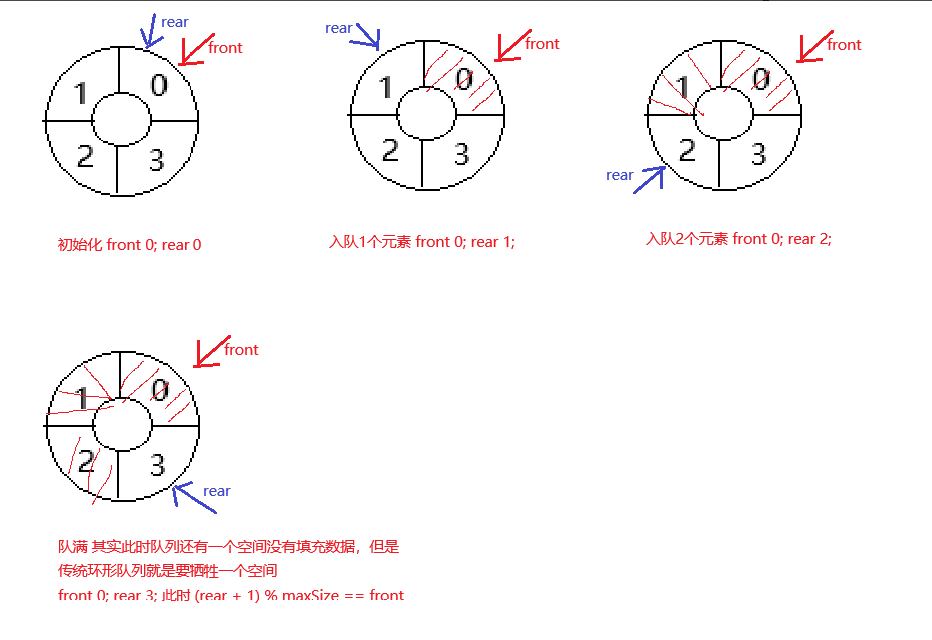
实现思路
- 所需的属性与简单队列无异
- 约定:队头指向队列的第一个元素(初始值为0),队尾指向队列最后一个元素的下一个位置(初始值为0)
- 传统实现环形队列的方式需要牺牲一个存储空间
完整代码
java/*** * 数组模拟环形队列(传统方式:牺牲一个存储空间) * * 约定:队头指向队列的第一个元素(初始值为0),队尾指向队列最后一个元素的下一个位置(初始值为0) **/ public class CircleArrayQueue { // 队列数据 private int[] data; // 队列最大长度 private int maxSize; // 头指针 private int front; // 尾指针 private int rear; // 判断队列是否已满 public boolean isFull() { return (rear + 1) % maxSize == front; } // 判断队列是否为空 public boolean isEmpty() { return rear == front; } // 入队 public void addQueue(int item) { if (isFull()) { throw new RuntimeException("队列已满,无法添加元素"); } data[rear] = item; // 考虑到环形的特性,rear指针不是简单地向后移动 rear = (rear + 1) % maxSize; } // 出队 public int getQueue() { if (isEmpty()) { throw new RuntimeException("队列为空,无法出队"); } int value = data[front]; // 考虑到环形的特性,front指针不是简单地向后移动 front = (front + 1) % maxSize; return value; } // 获取队头元素(只获取,不出队) public int getQueueHeadItem() { if (isEmpty()) { throw new RuntimeException("队列为空,无法获取队头元素"); } return data[front]; } // 获取元素个数 public int size() { return (rear + maxSize - front) % maxSize; } public CircleArrayQueue(int maxSize) { this.maxSize = maxSize; data = new int[maxSize]; front = 0; rear = 0; } }
数组实现环形队列(记录元素个数)
实现方式
- 传统方式元素的基础上,新增一个变量记录队列中元素的个数,通过此数值判断队列为空或满
- 约定:队头指向队列的第一个元素(初始值为-1),队尾指向队列最后一个元素(初始值为-1)
- 插入第一个元素后,rear正常按照环形特性赋值,front设置成第一个元素下标0
- 移除最后一个元素后,rear和front重置成 -1
完整代码
java/*** * 数组模拟环形队列(不牺牲空间,使用计数器记录队列元素个数) * * 约定:队头指向队列的第一个元素(初始值为-1),队尾指向队列最后一个元素(初始值为-1) **/ public class CircleArrayQueue02 { // 队列元素个数 private int count; // 队列数据 private int[] data; // 队列最大长度 private int maxSize; // 头指针 private int front; // 尾指针 private int rear; // 判断队列是否已满 public boolean isFull() { return count == maxSize; } // 判断队列是否为空 public boolean isEmpty() { return count == 0; } // 入队 public void addQueue(int item) { if (isFull()) { throw new RuntimeException("队列已满,无法添加元素"); } if (isEmpty()) { front = 0; } // 下一个元素的位置,考虑环形特性 rear = (rear + 1) % maxSize; // 元素入队 data[rear] = item; // 计数器加1 count++; } // 出队 public int getQueue() { if (isEmpty()) { throw new RuntimeException("队列为空,无法出队"); } // 当前元素的值 int value = data[front]; // 队列最后一个元素出队,重置头尾指针位置 if (count == 1) { rear = -1; front = -1; }else { // 队头向后移动一位,考虑环形特性 front = (front + 1) % maxSize; } // 计数器减1 count--; return value; } // 获取队头元素(只获取,不出队) public int getQueueHeadItem() { if (isEmpty()) { throw new RuntimeException("队列为空,无法获取队头元素"); } return data[front]; } // 获取元素个数 public int size() { return count; } public CircleArrayQueue02(int maxSize) { this.maxSize = maxSize; data = new int[maxSize]; front = -1; rear = -1; count = 0; } }
题外话
- 为什么传统方式实现的环形队列要牺牲一个存储空间?结合环形队列的约定来看,rear始终指向最后一个元素的下一个位置,这个位置要确保是空的,如果不牺牲最后一个空间,存储空间都满了,那rear指向的是data[0],此时front和rear指向的值相同,无法判断数组是空的还是满的(用front == rear判空)
- 不管是实现简单队列还是实现环形队列,记住约定结合图就能实现,环形队列只需要额外注意指针到达最大值后返回初始位置的问题(取余解决)
- 队列判空直接运用初始化队列时的数据就能判断
- 队列判满参考图和指针的位置
单链表
单链表分为带头节点和不带头节点的,带头节点的单链表插入第一个节点时和判断链表是否为空时更加方便
实现单链表需要定义两个类:结点类(用于存储数据和下一节点的地址)和单链表类(存储所有节点以及其他基本操作)
单链表的节点的插入、删除、修改操作实现方式
插入
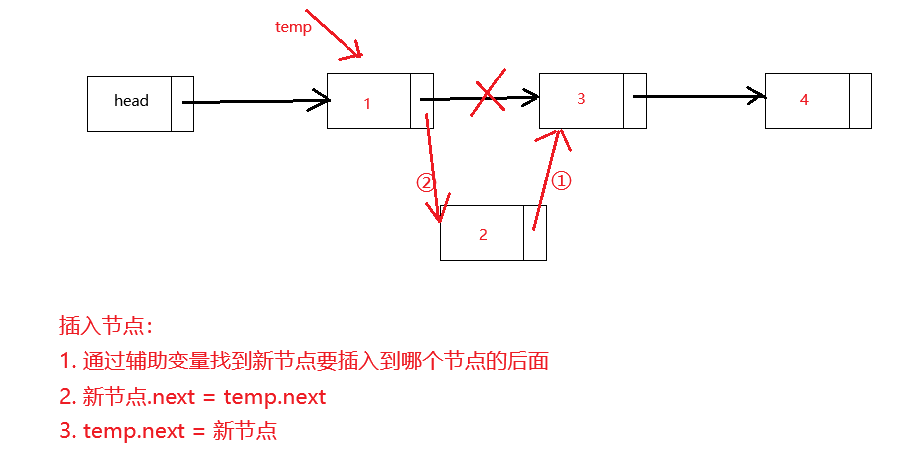
删除
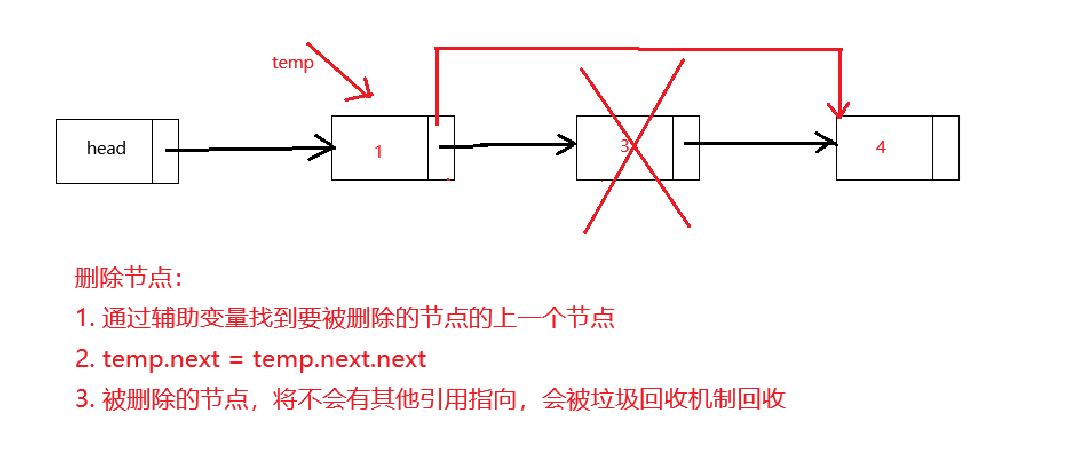
带头节点单链表demo
定义一个单链表,用来存放水浒传梁山好汉的信息,插入时不区分排名先后
定义一个单链表,用来存放水浒传梁山好汉的信息,插入时区分排名先后,并且如果排名相同,不允许插入
修改林冲节点的昵称为“懦夫”
删除晁盖节点
完整代码
java/*** * 单链表demo * * - 定义一个单链表,用来存放水浒传梁山好汉的信息,插入时不区分排名先后 * - 定义一个单链表,用来存放水浒传梁山好汉的信息,插入时区分排名先后 * - 修改林冲节点的昵称为“懦夫” * - 删除晁盖节点 **/ public class SingleLinkedListDemo { public static void main(String[] args) { SingleLinkedList liangshanpo = new SingleLinkedList(); HeroNode chaogai = new HeroNode(0, "晁盖", "托塔天王"); HeroNode songjiang = new HeroNode(1, "宋江", "及时雨"); HeroNode linchong = new HeroNode(2, "林冲", "豹子头"); HeroNode wuyong = new HeroNode(3, "吴用", "智多星"); HeroNode lujunyi = new HeroNode(5, "卢俊义", "玉麒麟"); // 测试单链表插入 // liangshanpo.addNode(lujunyi); // 5 // liangshanpo.addNode(chaogai); // 0 // liangshanpo.addNode(linchong); // 2 // liangshanpo.addNode(wuyong); // 3 // liangshanpo.addNode(songjiang); // 1 // liangshanpo.printAll(); // 测试单链表按照顺序插入 liangshanpo.addNodeByOrder(lujunyi); // 5 liangshanpo.addNodeByOrder(chaogai); // 0 liangshanpo.addNodeByOrder(linchong); // 2 liangshanpo.addNodeByOrder(wuyong); // 3 liangshanpo.addNodeByOrder(songjiang); // 1 liangshanpo.printAll(); System.out.println("============"); // 测试单链表节点修改 linchong.setNickName("懦夫"); liangshanpo.updateNode(linchong); liangshanpo.printAll(); System.out.println("============"); // 测试单链表节点删除 liangshanpo.deleteNode(chaogai); liangshanpo.printAll(); } } class SingleLinkedList { // 头节点 private final HeroNode head = new HeroNode(-1, "head", "头节点"); // 根据no删除节点 public void deleteNode(HeroNode heroNode) { HeroNode temp = head; while (true) { if (temp.getNext() == null) { break; } if (temp.getNext().getNo() == heroNode.getNo()) { temp.setNext(temp.getNext().getNext()); break; } temp = temp.getNext(); } } // 根据no修改节点内容 public void updateNode(HeroNode heroNode) { HeroNode temp = head; while (true) { if (temp.getNo() == heroNode.getNo()) { temp.setNickName(heroNode.getNickName()); break; } temp = temp.getNext(); } } // 按照顺序插入节点 public void addNodeByOrder(HeroNode heroNode) { HeroNode temp = head; while (true) { if (temp.getNext() == null) { // 首次插入,直接插入到头节点后面 temp.setNext(heroNode); break; }else { if (temp.getNo() < heroNode.getNo() && heroNode.getNo() < temp.getNext().getNo()) { heroNode.setNext(temp.getNext()); temp.setNext(heroNode); break; }else { temp = temp.getNext(); } } } } // 打印单链表 public void printAll() { HeroNode temp = head; while (true) { System.out.println(temp); if (temp.getNext() == null) { break; }else { temp = temp.getNext(); } } } // 找到最后一个节点,插入新节点到它后面(直接插入,不考虑排名先后) public void addNode(HeroNode heroNode) { // 在链表最后一个节点添加 HeroNode temp = head; while (true) { if (temp.getNext() == null) { break; } temp = temp.getNext(); } temp.setNext(heroNode); } } class HeroNode { private int no; private String name; private String nickName; private HeroNode next; public HeroNode(int no, String name, String nickName) { this.no = no; this.name = name; this.nickName = nickName; this.next = null; } public int getNo() { return no; } public void setNo(int no) { this.no = no; } public String getName() { return name; } public void setName(String name) { this.name = name; } public String getNickName() { return nickName; } public void setNickName(String nickName) { this.nickName = nickName; } public HeroNode getNext() { return next; } public void setNext(HeroNode next) { this.next = next; } @Override public String toString() { return "HeroNode{" + "no=" + no + ", name='" + name + '\'' + ", nickName='" + nickName + '\'' + '}'; } }
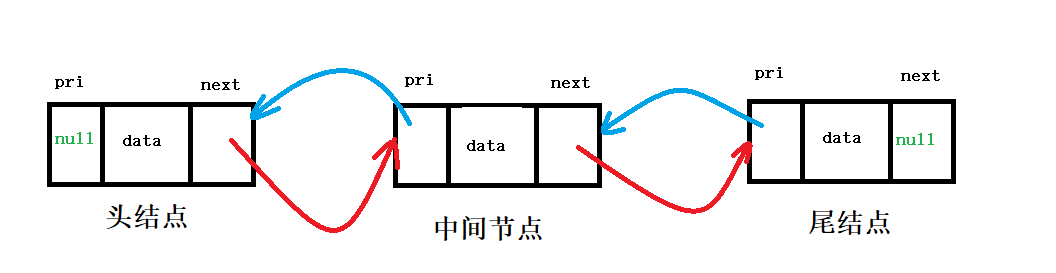
双向链表
双向链表的结构如图
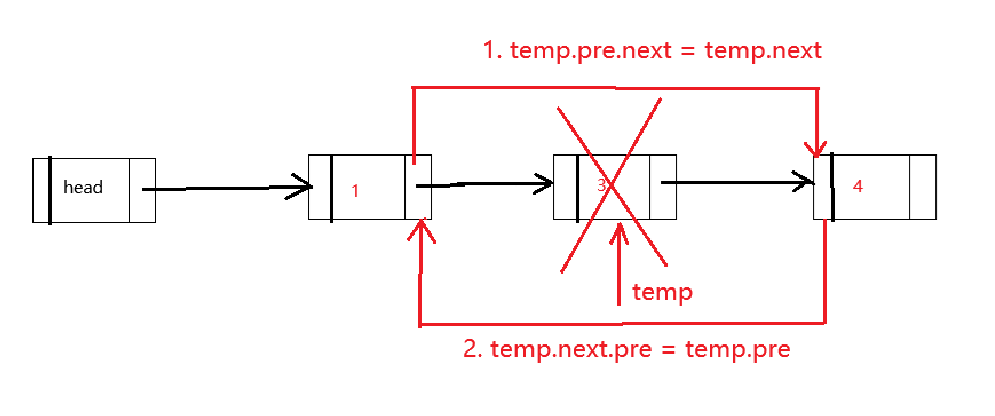
双向链表的自我删除
与单链表不同的是,单链表不管是插入还是删除操作,都需要找到目标节点的上一个节点进行操作,而双向链表删除节点时,只需要找到待删除的节点进行操作即可
实现思路
直接找到要删除的节点,如temp
temp.pre.next = temp.next
temp.next.pre = temp.pre,这一步要注意,temp后面可能没有元素,所以temp.next会报空指针
完整代码
javapublic class DoubleLinkedListDemo { public static void main(String[] args) { DoubleLinkedList list = new DoubleLinkedList(); Node node1 = new Node(); node1.setName("张三"); node1.setAge(20); Node node2 = new Node(); node2.setName("李四"); node2.setAge(21); Node node3 = new Node(); node3.setName("王五"); node3.setAge(22); list.addNode(node1); list.addNode(node3); list.addNode(node2); list.printAll(); System.out.println("========================"); list.deleteNode("王五"); list.printAll(); } } class DoubleLinkedList { private Node head = new Node(); // 根据条件删除节点 public void deleteNode(String name) { // 头节点没有名称,所以这里从头节点的下一个节点开始遍历 Node cur = head.getNext(); while (true) { if (cur.getName().equals(name)) { cur.getPrev().setNext(cur.getNext()); // 考虑如果要删除的节点是最后一个,则不需要执行下面的代码 if (cur.getNext() != null) { cur.getNext().setPrev(cur.getPrev()); } break; } cur = cur.getNext(); } } // 正向打印所有 public void printAll() { Node temp = head; while (true) { System.out.println(temp); if (temp.getNext() == null) { break; }else { temp = temp.getNext(); } } } // 添加节点(直接在尾部添加) public void addNode(Node node) { Node cur = head; while (true) { if (cur.getNext() == null) { cur.setNext(node); node.setPrev(cur); break; } cur = cur.getNext(); } } } class Node { private String name; private int age; private Node prev; private Node next; public Node() { this.prev = null; this.next = null; } public String getName() { return name; } public void setName(String name) { this.name = name; } public int getAge() { return age; } public void setAge(int age) { this.age = age; } public Node getPrev() { return prev; } public void setPrev(Node prev) { this.prev = prev; } public Node getNext() { return next; } public void setNext(Node next) { this.next = next; } @Override public String toString() { return "Node{" + "name='" + name + '\'' + ", age=" + age + '}'; } }
环形链表
- 定义:不管是环形单链表还是环形双向链表,都是最后一个节点指向第一个节点,形成一个闭环
环形单链表
示意图
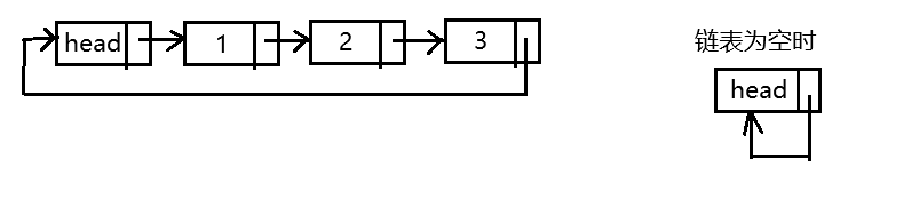
完整代码
javapublic class CircleSingleLinkedListDemo { public static void main(String[] args) { CircleSingleLinkedNode circleSingleLinkedNode01 = new CircleSingleLinkedNode(); circleSingleLinkedNode01.setName("张三"); circleSingleLinkedNode01.setAge(1); CircleSingleLinkedNode circleSingleLinkedNode02 = new CircleSingleLinkedNode(); circleSingleLinkedNode02.setName("李四"); circleSingleLinkedNode02.setAge(2); CircleSingleLinkedNode circleSingleLinkedNode03 = new CircleSingleLinkedNode(); circleSingleLinkedNode03.setName("王五"); circleSingleLinkedNode03.setAge(3); CircleSingleLinkedList circleLinkedList = new CircleSingleLinkedList(); circleLinkedList.addNode(circleSingleLinkedNode01); circleLinkedList.addNode(circleSingleLinkedNode03); circleLinkedList.addNode(circleSingleLinkedNode02); System.out.println("链表长度(不包含头节点)=====》" + circleLinkedList.size()); circleLinkedList.printAll(); circleLinkedList.deleteNode(circleSingleLinkedNode03); System.out.println("删除节点后======》"); System.out.println("链表长度(不包含头节点)=====》" + circleLinkedList.size()); circleLinkedList.printAll(); } } class CircleSingleLinkedList { // 有头节点的环形列表,头节点不做任何修改,确保环形列表始终能找到头节点 private CircleSingleLinkedNode head = new CircleSingleLinkedNode(); // 删除节点 // 环形单链表的本质上还是一个单链表,所以删除节点时,只需要找到要删除节点的前一个节点进行操作即可 public void deleteNode(CircleSingleLinkedNode circleSingleLinkedNode) { CircleSingleLinkedNode cur = head; if (size() == 0) { System.out.println("链表为空,无法删除节点"); return; } while (true) { if (cur.getNext() == circleSingleLinkedNode) { cur.setNext(cur.getNext().getNext()); break; }else { cur = cur.getNext(); } } } // 获取环形链表长度 public int size() { // 从非头节点的第一个值开始 CircleSingleLinkedNode temp = head.getNext(); // 链表为空 if (head.getNext() == head) { return 0; } int size = 0; while (true) { size++; // 最后一个节点时退出循环 if (temp.getNext() == head) { break; }else { temp = temp.getNext(); } } return size; } // 正向打印所有 public void printAll() { CircleSingleLinkedNode temp = head; while (true) { System.out.println(temp); if (temp.getNext() == head) { break; }else { temp = temp.getNext(); } } } // 在环形列表最后面添加节点 public void addNode(CircleSingleLinkedNode circleSingleLinkedNode) { CircleSingleLinkedNode cur = head; // 如果环形链表为空,直接添加 if (size() == 0) { head.setNext(circleSingleLinkedNode); circleSingleLinkedNode.setNext(head); } while (true) { // 找到最后一个节点(最后一个节点.next = head) if (cur.getNext() == head) { cur.setNext(circleSingleLinkedNode); circleSingleLinkedNode.setNext(head); break; }else { cur = cur.getNext(); } } } } class CircleSingleLinkedNode { private CircleSingleLinkedNode next; private String name; private int age; public CircleSingleLinkedNode getNext() { return next; } public void setNext(CircleSingleLinkedNode next) { this.next = next; } public String getName() { return name; } public void setName(String name) { this.name = name; } public int getAge() { return age; } public void setAge(int age) { this.age = age; } public CircleSingleLinkedNode() { this.next = this; } @Override public String toString() { return "Node{" + "name='" + name + '\'' + ", age=" + age + '}'; } }
环形双向链表
示意图
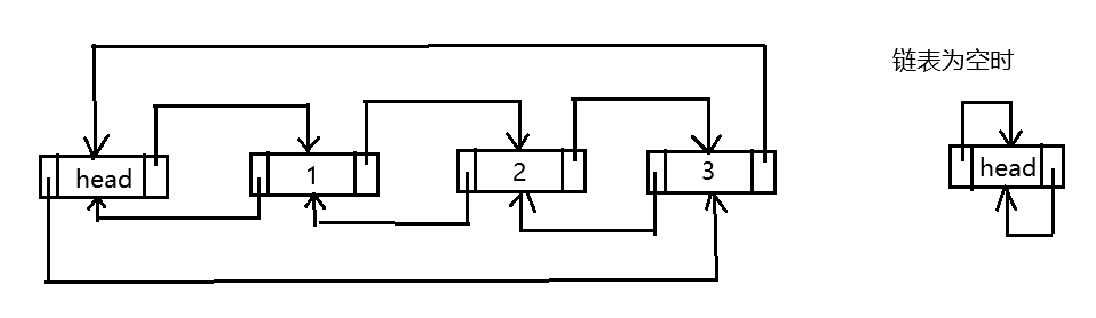
完整代码
javapublic class CircleDoubleLinkedListDemo { public static void main(String[] args) { CircleDoubleLinkedNode node1 = new CircleDoubleLinkedNode(); node1.setName("Tom"); node1.setAge(20); CircleDoubleLinkedNode node2 = new CircleDoubleLinkedNode(); node2.setName("Jerry"); node2.setAge(21); CircleDoubleLinkedNode node3 = new CircleDoubleLinkedNode(); node3.setName("Jack"); node3.setAge(30); CircleDoubleLinkedList circleDoubleLinkedList = new CircleDoubleLinkedList(); circleDoubleLinkedList.addNode(node1); circleDoubleLinkedList.addNode(node2); circleDoubleLinkedList.addNode(node3); System.out.println("链表长度(不包含头节点)=====》" + circleDoubleLinkedList.size()); System.out.println("正向打印所有节点=====》"); circleDoubleLinkedList.printAll(); System.out.println("反向打印所有节点=====》"); circleDoubleLinkedList.printAllReverse(); System.out.println("删除jerry节点=====》"); circleDoubleLinkedList.deleteNode(node2); System.out.println("链表长度(不包含头节点)=====》" + circleDoubleLinkedList.size()); System.out.println("正向打印所有节点=====》"); circleDoubleLinkedList.printAll(); } } class CircleDoubleLinkedList { private CircleDoubleLinkedNode head = new CircleDoubleLinkedNode(); // 删除节点 // 环形单链表的本质上还是一个双链表,所以删除节点时,只需要找到要删除节点进行操作即可 public void deleteNode(CircleDoubleLinkedNode circleDoubleLinkedNode) { if (size() == 0) { System.out.println("链表为空,无法删除"); return; } CircleDoubleLinkedNode cur = head.getNext(); while (true) { // cur是待删除的节点 if (cur == circleDoubleLinkedNode) { cur.getPre().setNext(cur.getNext()); cur.getNext().setPre(cur.getPre()); break; }else { cur = cur.getNext(); } } } // 添加节点 public void addNode(CircleDoubleLinkedNode circleDoubleLinkedNode) { if (size() == 0) { head.setNext(circleDoubleLinkedNode); circleDoubleLinkedNode.setPre(head); circleDoubleLinkedNode.setNext(head); head.setPre(circleDoubleLinkedNode); return; } CircleDoubleLinkedNode cur = head; while (true) { // cur是最后一个节点 if (cur.getNext() == head && head.getPre() == cur) { cur.setNext(circleDoubleLinkedNode); circleDoubleLinkedNode.setPre(cur); circleDoubleLinkedNode.setNext(head); head.setPre(circleDoubleLinkedNode); break; }else { cur = cur.getNext(); } } } // 获取环形双向链表的长度 public int size() { int count = 0; if (head.getNext() == head && head.getPre() == head) { return 0; } CircleDoubleLinkedNode cur = head.getNext(); while (true) { count++; if (cur.getNext() == head && head.getPre() == cur) { break; }else { cur = cur.getNext(); } } return count; } // 反向打印所有 public void printAllReverse() { CircleDoubleLinkedNode temp = head.getPre(); while (true) { System.out.println(temp); if (temp.getPre() == head) { break; }else { temp = temp.getPre(); } } } // 正向打印所有 public void printAll() { CircleDoubleLinkedNode temp = head.getNext(); while (true) { System.out.println(temp); if (temp.getNext() == head) { break; }else { temp = temp.getNext(); } } } } class CircleDoubleLinkedNode { private CircleDoubleLinkedNode pre; private CircleDoubleLinkedNode next; private String name; private int age; public CircleDoubleLinkedNode() { this.pre = this; this.next = this; } public CircleDoubleLinkedNode getPre() { return pre; } public void setPre(CircleDoubleLinkedNode pre) { this.pre = pre; } public CircleDoubleLinkedNode getNext() { return next; } public void setNext(CircleDoubleLinkedNode next) { this.next = next; } public String getName() { return name; } public void setName(String name) { this.name = name; } public int getAge() { return age; } public void setAge(int age) { this.age = age; } @Override public String toString() { return "CircleDoubleLinkedNode{" + "name='" + name + '\'' + ", age=" + age + '}'; } }
约瑟夫问题
问题描述:设编号为1,2,… n的n个人围坐一圈,约定编号为k(1<=k<=n)的人从1开始报数,数到m 的那个人出列,它的下一位又从1开始报数,数到m的那个人又出列,依次类推,直到所有人出列为止,由此产生一个出队编号的序列。
实现思路
- 创建一个 不带头节点 的环形单链表
- 添加元素时,如果是第一次添加,就设置成头节点
- 找到起始位置
- 设置一个记录位移步数的变量,每次移动时步数加1
- 找到 位移步数 = m -1(数到m,但是本身是从1开始) -1(目标节点的上一个位置) 的位置
- 移除节点,重置步数计数器
完整代码
javapublic class InterviewExercise01 { public static void main(String[] args) { JosephNode node01 = new JosephNode(); node01.setNo(1); node01.setName("张三"); JosephNode node02 = new JosephNode(); node02.setNo(2); node02.setName("李四"); JosephNode node03 = new JosephNode(); node03.setNo(3); node03.setName("王五"); JosephNode node04 = new JosephNode(); node04.setNo(4); node04.setName("王二麻子"); JosephNode node05 = new JosephNode(); node05.setNo(5); node05.setName("赵六"); JosephLinkedList circleLinkedList = new JosephLinkedList(); circleLinkedList.addNode(node01); circleLinkedList.addNode(node02); circleLinkedList.addNode(node03); circleLinkedList.addNode(node04); circleLinkedList.addNode(node05); circleLinkedList.printAll(); System.out.println("======================"); circleLinkedList.solve(circleLinkedList, 1, 2); } } class JosephLinkedList { private JosephNode head = null; // 解决约瑟夫问题 public void solve(JosephLinkedList josephLinkedList, int k, int m) { // 临时头节点 JosephNode tempHead = new JosephNode(); // 临时最后一个节点 JosephNode temp = tempHead; int steps = 0; JosephNode cur = head; // 找到起始位置 for (int i = 0; i < k - 1; i++) { cur = cur.getNext(); } System.out.println("起始位置:" + cur); while (true) { // 如果链表只剩一个节点,结束循环 if (cur.getNext() == cur) { cur.setNext(null); temp.setNext(cur); break; } // 待删除节点的上一个节点 if (steps == (m - 2)) { // 将待删除节点拼接到临时头节点的后面 temp.setNext(cur.getNext()); temp = temp.getNext(); // 删除节点 cur.setNext(cur.getNext().getNext()); // 重新定位 cur = cur.getNext(); steps = 0; }else { cur = cur.getNext(); steps++; } } // 打印结果 JosephNode t = tempHead.getNext(); while (true) { if (t != null) { System.out.println(t); t = t.getNext(); }else { break; } } } // 正向打印所有 public void printAll() { JosephNode temp = head; while (true) { System.out.println(temp); if (temp.getNext() == head) { break; }else { temp = temp.getNext(); } } } // 添加节点 public void addNode(JosephNode josephNode) { if (head == null) { head = josephNode; head.setNext(head); return; } JosephNode cur = head; while (true) { // 最后一个节点 if (cur.getNext() == head) { cur.setNext(josephNode); josephNode.setNext(head); break; }else { cur = cur.getNext(); } } } } class JosephNode { private int no; private String name; private JosephNode next; public JosephNode getNext() { return next; } public void setNext(JosephNode next) { this.next = next; } public String getName() { return name; } public void setName(String name) { this.name = name; } public int getNo() { return no; } public void setNo(int no) { this.no = no; } @Override public String toString() { return "JosephNode{" + "no=" + no + "name='" + name + '\'' + '}'; } }
链表设置头节点的好处

栈
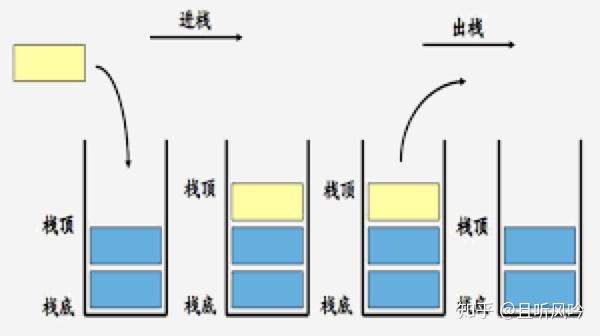
定义:栈是一种只允许在表尾进行插入和删除的线性表,元素秉承着先入后出(FILO)的原则
顺序栈示意图
链表栈示意图
使用数组实现顺序栈
实现思路
- 定义栈的最大长度,栈顶(栈顶始终指向栈尾元素,初始值 -1),元素存储数组
- 入栈:top++; data[top] = newValue;
- 出栈:value = data[top]; top--; return value;
完整代码
javapublic class ArrayStackDemo { public static void main(String[] args) { ArrayStack stack = new ArrayStack(10); // 栈从顶到底的顺序 6 5 4 3 2 1 stack.push(1); stack.push(2); stack.push(3); stack.push(4); stack.push(5); stack.push(6); stack.printStack(); // 出栈 stack.pop(); System.out.println("出栈后====》"); stack.printStack(); } } class ArrayStack { private int maxSize; // 栈的最大长度 private int[] data; // 数据 private int top = -1; // 栈顶指针 // 打印 public void printStack() { for (int i = top; i >= 0; i--) { System.out.println(data[i]); } } // 出栈 public int pop() { if (isEmpty()) { throw new RuntimeException("栈空,无法删除"); } int value = data[top]; top--; return value; } // 入栈 public void push(int newValue) { // 判断栈是否满 if (isFull()) { throw new RuntimeException("栈满,无法添加"); } top++; data[top] = newValue; } // 判断栈是否满 public boolean isFull(){ return maxSize - 1 == top; } // 判断栈是否为空 public boolean isEmpty() { return top == -1; } public ArrayStack(int maxSize) { this.maxSize = maxSize; this.data = new int[maxSize]; } }
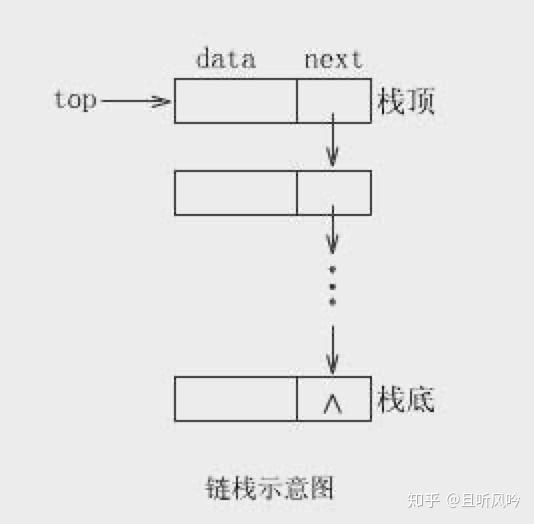
使用单链表实现链表栈
实现思路:使用 头插法入栈,头删法出栈 实现栈的入和出
完整代码
javapublic class SingleLinkedListStackDemo { public static void main(String[] args) { SingleLinkedListStack stack = new SingleLinkedListStack(); stack.push(new Node(1)); stack.push(new Node(2)); stack.push(new Node(3)); stack.push(new Node(4)); // 打印栈 stack.printStack(); // 出栈 stack.pop(); System.out.println("出栈后=======>"); stack.printStack(); } } class SingleLinkedListStack { private Node head = new Node(-1); public void printStack() { Node cur = head.getNext(); while(true) { if (cur == null) { break; }else { System.out.println(cur); cur = cur.getNext(); } } } // 出栈 public Node pop() { if (isEmpty()) { throw new RuntimeException("栈空,无法出栈"); } Node firstNode = head.getNext(); head.setNext(head.getNext().getNext()); return firstNode; } // 入栈(采用头插法) public void push(Node newNode) { Node firstNode = head.getNext(); head.setNext(newNode); newNode.setNext(firstNode); } // 判断栈是否为空 public boolean isEmpty() { return head.getNext() == null; } } class Node { private Node next; private int value; public Node(int value) { this.value = value; } public Node getNext() { return next; } public void setNext(Node next) { this.next = next; } public int getValue() { return value; } public void setValue(int value) { this.value = value; } @Override public String toString() { return "Node{" + "value=" + value + '}'; } }
前缀(波兰)/中缀/后缀(逆波兰)表达式
定义
- 前缀表达式:运算符位于操作数之前,如(1+2) * 3 - 4对应的前缀表达式为 - * + 1 2 3 4
- 中缀表达式:即(1+2) * 3 - 4,对于人类来说方便计算,但是对于计算机来说不好操作,通常会将中缀表达式转为后缀表达式(常见操作)或者前缀表达式后进行求值
- 后缀表达式:运算符位于操作数之后,如(1+2) * 3 - 4对应的后缀表达式为 1 2 + 3 * 4 -
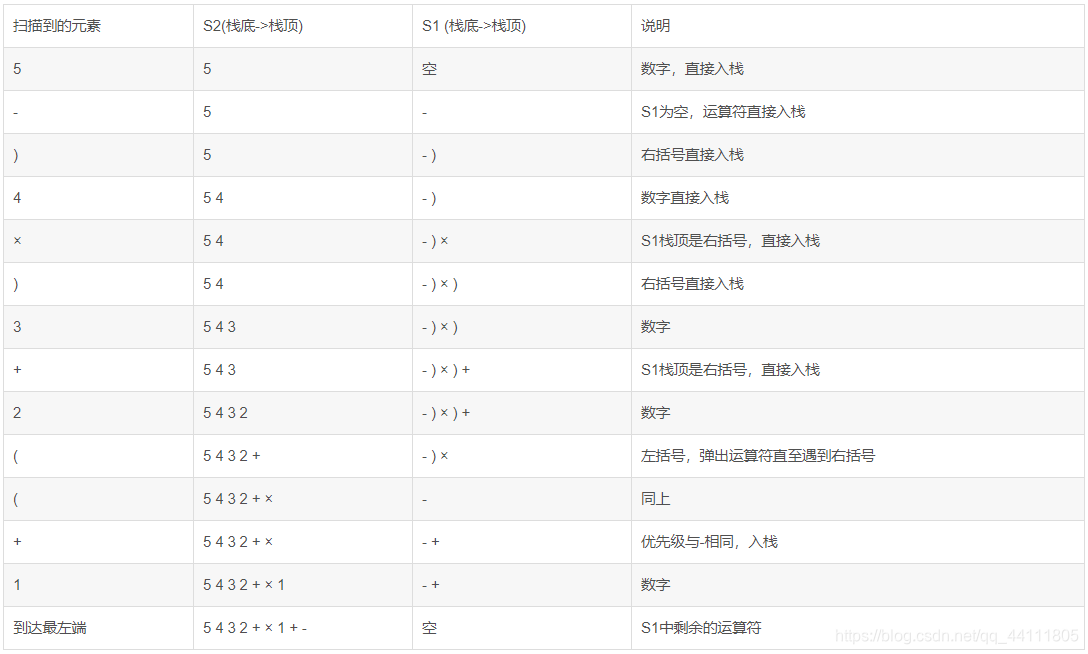
中缀表达式转前缀表达式步骤
- 初始化两个栈:运算符栈S1和储存中间结果的栈S2
- 从右至左扫描中缀表达式
- 遇到数字时,将其压入S2
- 遇到运算符时,比较其与S1栈顶运算符的优先级
- 如果S1为空,或者S1栈顶运算符为右括号,则将此运算符入栈
- 如果此运算符的优先级 >= S1栈顶元素,则将此运算符入栈
- 否则,将S1栈顶的运算符弹出压到S2中,并再次跳到第一步继续比较
- 遇到括号时
- 如果是右括号,直接压入S1
- 如果是左括号,依次弹出S1栈顶的运算符并压入S2,直到S1栈顶遇到右括号弹出(舍弃)结束
- 将S1剩余的运算符依次弹出并压入S2
- 此时S2依次弹出的元素顺序(栈顶->栈底)就是前缀表达式的顺序
前缀表达式在计算机上求值步骤
- 从右到左扫描前缀表达式,1)遇到数字就压入数字栈 2)遇到运算符,弹出栈顶元素和次栈顶元素
- 栈顶元素 运算符 次栈顶元素,得到结果后,压入数字栈
- 最后数字栈的栈顶元素即为计算结果
中缀表达式转前缀表达式并计算值
示例:中缀表达式 1+((2+3)x4)-5 转换成前缀表达式的过程如下
完整代码
javapublic class PrefixExpressionDemo { // 前缀表达式求值 public static int getPrefixExpressionResult(String prefixExpression) { // 从右到左扫描前缀表达式 = 表达式逆向后从左到右扫描 String reverseExpression = new StringBuilder(prefixExpression).reverse().toString(); // 数字栈 Stack<Integer> numStack = new Stack<>(); for (int i = 0; i < reverseExpression.length(); i++) { String item = reverseExpression.substring(i, i+1); // 遇到数字直接入数字栈 if (item.matches("\\d+")) { numStack.push(Integer.parseInt(item)); }else if (item.matches("[\\+|\\-|\\*|\\/]")) { // 遇到运算符,弹出两个数字栈顶元素进行计算 int top = numStack.pop(); int secondTop = numStack.pop(); switch (item) { case "+": numStack.push(top + secondTop); break; case "-": numStack.push(top - secondTop); break; case "*": numStack.push(top * secondTop); break; case "/": numStack.push(top / secondTop); break; } } } return numStack.pop(); } // 运算符栈 private static Stack<String> s1 = new Stack<>(); // 中间结果栈 private static Stack<String> s2 = new Stack<>(); public static void handleScanItem(String item) { // 遇到数字直接入s2栈 if (item.matches("\\d+")) { s2.push(item); return; } // 遇到运算符 if (item.matches("[\\+|\\-|\\*|\\/]")) { // 如果s1栈为空 || s1栈顶元素为右括号 直接入s1 if (s1.isEmpty() || ")".equals(s1.peek())) { s1.push(item); return; } // 如果此运算符的优先级 >= s1栈顶运算符的优先级 直接入s1 if ( ("*".equals(item) || "/".equals(item)) || (("+".equals(item) || "-".equals(item)) && ("+".equals(s1.peek()) || "-".equals(s1.peek()))) ) { s1.push(item); return; } // 否则将s1栈顶元素弹出并入s2,并继续比较当前运算符 String s1Pop = s1.pop(); s2.push(s1Pop); handleScanItem(item); } // 遇到右括号,直接压入s1栈 if (item.equals(")")) { s1.push(item); return; } // 遇到左括号 if (item.equals("(")) { String s1Pop; s1Pop = s1.pop(); s2.push(s1Pop); while (true) { if (s1.peek().equals(")")) { s1.pop(); break; }else { s1Pop = s1.pop(); s2.push(s1Pop); } } } } // 中缀表达式转前缀表达式 public static String infixToPrefixExpression(List<String> infixExpressionList) { StringBuilder prefixExpression = new StringBuilder(); for (int i = infixExpressionList.size() - 1; i >= 0; i--) { String item = infixExpressionList.get(i); // 处理当前字符 handleScanItem(item); } while (!s1.isEmpty()) { s2.push(s1.pop()); } while (!s2.isEmpty()) { prefixExpression.append(s2.pop()); } return prefixExpression.toString(); } public static void main(String[] args) { List<String> infixExpressionList = Arrays.asList("1 + ( ( 2 + 3 ) * 4 ) - 5".split(" ")); System.out.println("前缀表达式为:" + infixToPrefixExpression(infixExpressionList)); System.out.println("前缀表达式求值为:" + getPrefixExpressionResult(infixToPrefixExpression(infixExpressionList))); } }
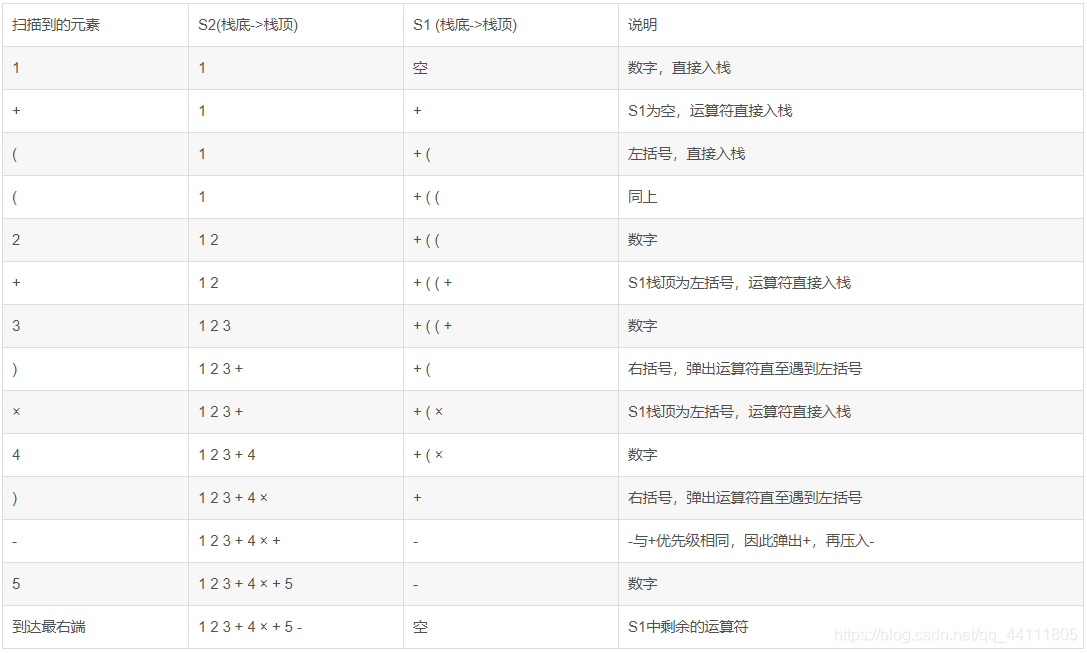
中缀表达式转后缀表达式步骤
- 初始化两个栈:运算符栈S1和储存中间结果的栈S2
- 从左到右扫描中缀表达式
- 遇到数字时,将其压入S2
- 遇到运算符时,比较其与S1栈顶运算符的优先级
- 如果S1为空,或者S1栈顶运算符为左括号,则将此运算符入栈
- 如果此运算符的优先级 > S1栈顶元素,则将此运算符入栈
- 否则,将S1栈顶的运算符弹出压到S2中,并再次跳到第一步继续比较
- 遇到括号时
- 如果是左括号,直接压入S1
- 如果是右括号,依次弹出S1栈顶的运算符并压入S2,直到S1栈顶遇到左括号弹出(舍弃)结束
- 将S1剩余的运算符依次弹出并压入S2
- 此时S2依次弹出的元素顺序的逆序(栈底->栈顶)就是后缀表达式的顺序
后缀表达式在计算机上求值步骤
- 从左到右扫描前缀表达式,1)遇到数字就压入数字栈 2)遇到运算符,弹出栈顶元素和次栈顶元素
- 次栈顶元素 运算符 栈顶元素,得到结果后,压入数字栈
- 最后数字栈的栈顶元素即为计算结果
中缀表达式转后缀表达式并计算值
示例:中缀表达式 1+((2+3)x4)-5 转换成后缀表达式的过程如下
完整代码
javapublic class SuffixExpressionDemo { // 运算符栈 private static Stack<String> s1 = new Stack<>(); // 中间结果栈 private static Stack<String> s2 = new Stack<>(); // 后缀表达式求值 public static int getSuffixExpressionResult(String suffixExpression) { // 数字栈 Stack<Integer> numStack = new Stack<>(); // 从左到右扫描表达式 for (int i = 0; i < suffixExpression.length(); i++) { String item = suffixExpression.substring(i, i + 1); // 遇到数字直接入数字栈 if (item.matches("\\d+")) { numStack.push(Integer.parseInt(item)); }else if (item.matches("[\\+|\\-|\\*|\\/]")) { // 遇到运算符,弹出两个数字栈顶元素进行计算 int top = numStack.pop(); int secondTop = numStack.pop(); switch (item) { case "+": numStack.push(secondTop + top); break; case "-": numStack.push(secondTop - top); break; case "*": numStack.push(secondTop * top); break; case "/": numStack.push(secondTop / top); break; } } } return numStack.pop(); } public static void handleScanItem(String item) { // 遇到数字直接入s2栈 if (item.matches("\\d+")) { s2.push(item); return; } // 遇到运算符 if (item.matches("[\\+|\\-|\\*|\\/]")) { // 如果s1栈为空 || s1栈顶元素为左括号 直接入s1 if (s1.isEmpty() || "(".equals(s1.peek())) { s1.push(item); return; } // 如果此运算符的优先级 > s1栈顶运算符的优先级 直接入s1 if ( ("*".equals(item) || "/".equals(item)) && ("+".equals(s1.peek()) || "-".equals(s1.peek())) ) { s1.push(item); return; } // 否则将s1栈顶元素弹出并入s2,并继续比较当前运算符 String s1Pop = s1.pop(); s2.push(s1Pop); handleScanItem(item); } // 遇到左括号,直接压入s1栈 if (item.equals("(")) { s1.push(item); return; } // 遇到右括号 if (item.equals(")")) { String s1Pop; s1Pop = s1.pop(); s2.push(s1Pop); while (true) { if (s1.peek().equals("(")) { s1.pop(); break; }else { s1Pop = s1.pop(); s2.push(s1Pop); } } } } // 中缀表达式转后缀表达式 public static String infixToSuffixExpression(List<String> infixExpressionList) { for (int i = 0; i < infixExpressionList.size(); i++) { String item = infixExpressionList.get(i); // 处理当前字符 handleScanItem(item); } while (!s1.isEmpty()) { s2.push(s1.pop()); } StringBuilder sb = new StringBuilder(); while (!s2.isEmpty()) { sb.append(s2.pop()); } // 栈的逆序结果就是后缀表达式 return sb.reverse().toString(); } public static void main(String[] args) { List<String> infixExpressionList = Arrays.asList("1 + ( ( 2 + 3 ) * 4 ) - 5".split(" ")); System.out.println("后缀表达式为:" + infixToSuffixExpression(infixExpressionList)); System.out.println("后缀表达式求值为:" + getSuffixExpressionResult(infixToSuffixExpression(infixExpressionList))); } }